Ինչպես հաշվարկել ճկման նպաստը ձեր սեղմման արգելակի համար

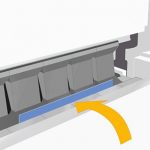
1. Հասկանալով ճկման գործընթացը. պարզ փաստեր

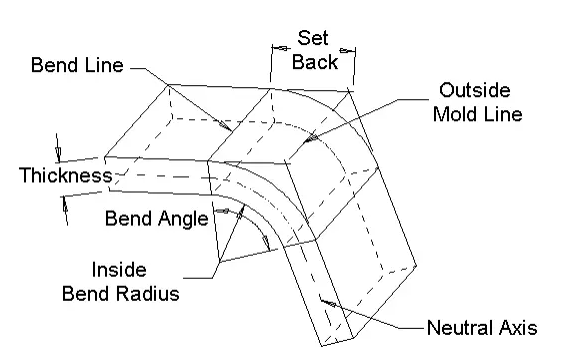
Ճկման թույլտվություն = Անկյուն * (T/ 180)* (շառավիղ + K-գործոն *Հաստություն) Կռվածքի փոխհատուցում = Կռման թույլտվություն-(2 * ետ վերադարձ)

Ներսից հետք = արևայրուք (Անկյուն / 2) *Շառավիղ դրսից թիկունք = արևայրուք (անկյուն / 2)*(շառավիղ + հաստություն)

1) Կռացած մասի վրա ստացված շառավիղը ազդում է այն երկարության վրա, որով պետք է կտրենք այդ հատվածը (մինչև կռելը):

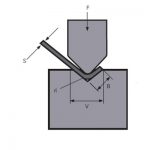
2) Ճկման ժամանակ ստացված շառավիղը 99%-ով կախված է V բացվածքից, որի հետ մենք ընտրում ենք աշխատել:

Նախքան մասը նախագծելը և, անշուշտ, նախքան բլանկները կտրելը, մենք ՊԵՏՔ Է ՀԻՄՆԱԼ իմանանք, թե ինչ V բացվածքով կծկենք հատվածը սեղմիչ արգելակի վրա:

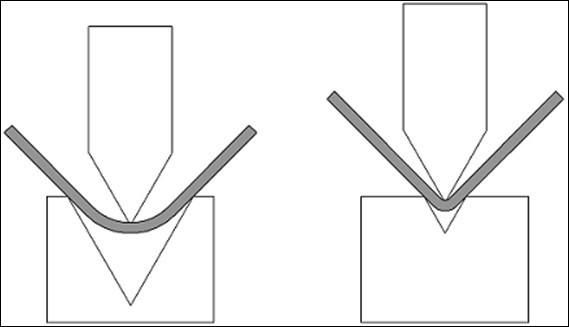
2. Ինչպես է շառավիղը ազդում բլանկների վրա

ավելի մեծ շառավիղը «մղելու» է մեր հատվածի ոտքերը դեպի դրսը՝ տպավորություն ստեղծելով, որ բլանկը «չափազանց երկար» է կտրվել։

ավելի փոքր շառավիղը կպահանջի դատարկ, որը պետք է կտրվի «մի փոքր ավելի երկար», քան եթե շառավիղն ավելի մեծ լիներ:

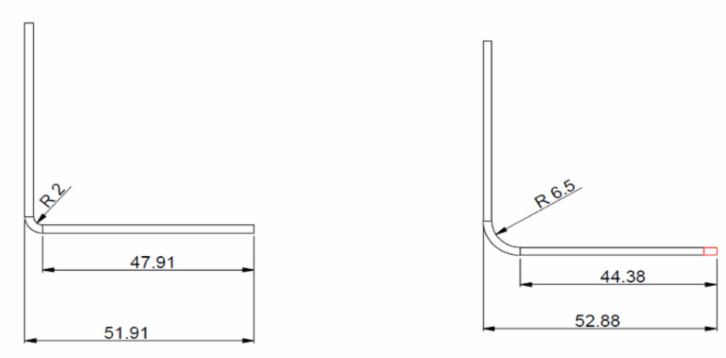
3. Ճկման նպաստ

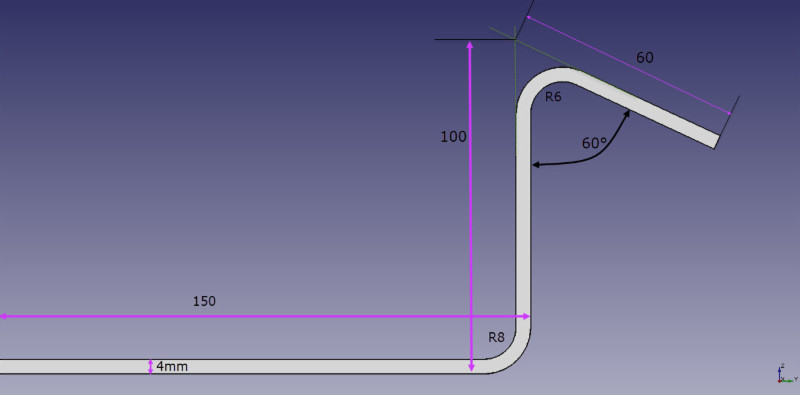
Վերոնշյալ նկարի բացված բացերը կհաշվարկվեն հետևյալ կերպ.

B = 150 + 100 + 60 + BA1 + BA2

Ինչպես հաշվարկել BA1 և BA2:

Ճկման նպաստի հաշվարկ

Այն մասնաբաժինը, որը մենք պետք է կրճատենք երկու ոտքերից, երբ համընկնում են՝ դառնալով հարթ, այն է, ինչը մենք սովորաբար գիտենք որպես «ճկման նպաստ» (կամ BA հավասարման մեջ):

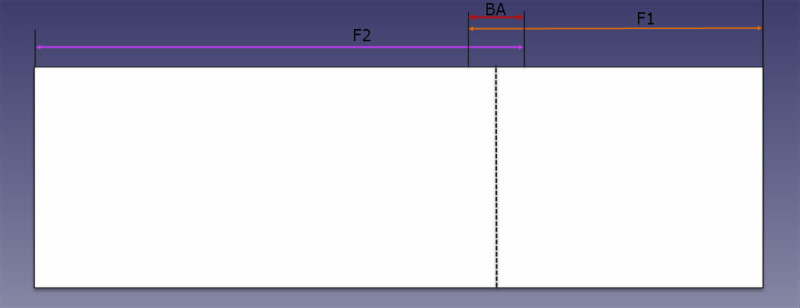
Ճկման նպաստի բանաձև

BA բանաձեւը մինչև 90° թեքությունների համար

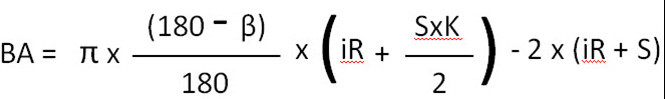
BA բանաձև 91°-ից մինչև 165° թեքությունների համար

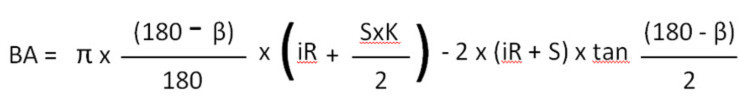
iR= Ներքին շառավիղ
S=հաստություն
Β = անկյուն
Π = 3,14159265….
K = K գործոն

K գործոն

Մամլիչ արգելակի վրա կռանալիս թիթեղի ներքին մասը սեղմվում է, իսկ արտաքին մասը երկարացվում է:

Սա նշանակում է, որ կա թերթիկի մի հատված, որտեղ մանրաթելերը ոչ սեղմված են, ոչ երկարաձգված: Մենք այս հատվածն անվանում ենք «չեզոք առանցք»:

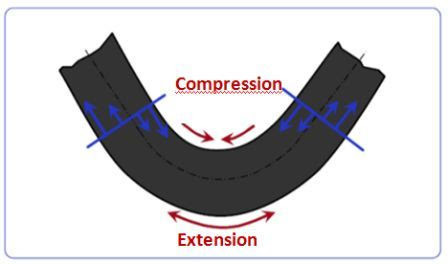
Կռվածքի ներսից մինչև չեզոք առանցքի հեռավորությունը այն է, ինչ մենք անվանում ենք K գործոն:
Այս արժեքը գալիս է այն նյութի հետ, որը մենք գնում ենք, և այն չի կարող փոխվել:
Այս արժեքը արտահայտվում է կոտորակներով: Որքան փոքր է K գործակիցը, այնքան չեզոք առանցքը մոտ կլինի թերթի ներքին շառավղին:

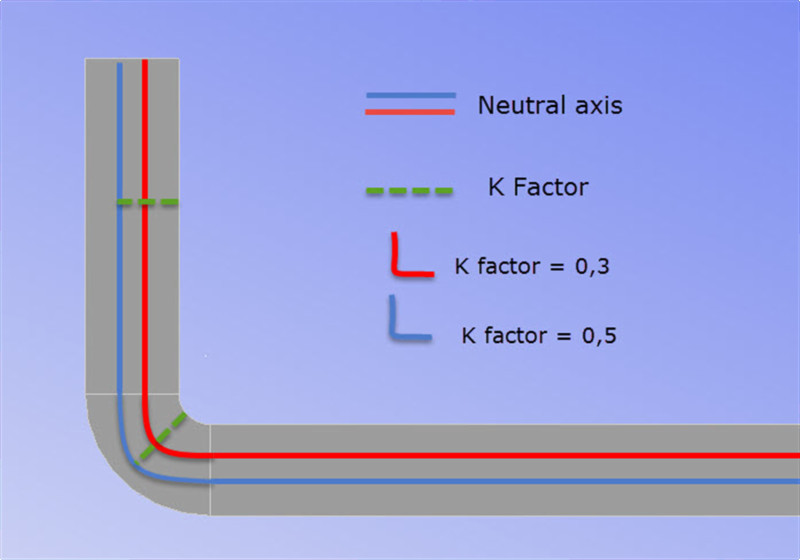
K գործոն = նուրբ կարգավորում

K գործոնը ազդում է մեր բացված դատարկի վրա: Ոչ այնքան, որքան մասի շառավիղը, բայց մենք կարող ենք դա պատկերացնել որպես բլանկների համար ճշգրիտ թյունինգ հաշվարկներ:

որքան փոքր է K գործոնը, այնքան ավելի շատ նյութ է տարածվում և, հետևաբար, «դուրս է մղվում»: ինչը նշանակում է, որ մեր ոտքը կդառնա «մեծ»:

K գործոնի գնահատում

Ժամանակի մեծ մասը մենք կարող ենք գնահատել և կարգավորել K գործակիցը մեր դատարկ հաշվարկները լավ կարգավորելիս:
մեզ անհրաժեշտ է ընդամենը մի քանի թեստեր (ընտրված V բացվածքի վրա) և չափել մասի շառավիղը:
Այն դեպքում, երբ դուք պետք է որոշեք ավելի ճշգրիտ K գործակիցը, ստորև ներկայացված է ձեր թեքության համար ճշգրիտ K գործակիցը որոշելու հաշվարկը:

K գործոն՝ բանաձև

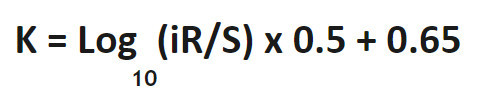
Օրինակի լուծում.

B = 150 + 100 + 60 +BA1 + BA2

K գործոնի գնահատում

B1՝ R/S=2 => K=0,8
B2՝ R/S=1,5 => K=0,8
Երկու ոլորաններն էլ 90° կամ պակաս են.

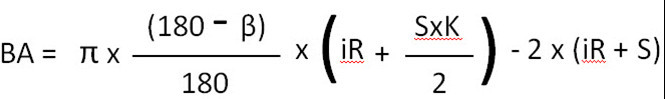
ինչը նշանակում է:

B1 = 3,14 x 0,66 x (6 + ((4×0,8)/2) – 2 x 10
B1 = -4,25
B2 = 3,14 x 0,5 x (8 + ((4×0,8)/2) – 2 x 12
B2 = -8,93

հետևաբար.
B = 150 + 100 + 60 + (-4,25) + (-8,93)
B= 296,8 մմ